绪 论 一、《建筑力学》的研究对象 在建筑物中承受并传递荷载而起骨架作用的部分叫做建筑结构,简称结构。组成结构的单个物体叫构件。构件一般分三类,即杆件、薄壁构件和实体构件。在结构中应用较多的是杆件。 对土建类专业来讲,《建筑力学》的主要研究对象就是杆件和杆件结构。 二、《建筑力学》的主要任务 《建筑力学》的任务就是为解决安全和经济这一矛盾提供必要的理论基础和计算方法。 三、《建筑力学》的内容简介 第一部分讨论力系的简化、平衡及对构件(或结构)进行受力分析的基本理论和方法;第二部分讨论构件受力后发生变形时的承载力问题。为设计即安全又经济的结构构件选择适当的材料、截面形状和尺寸,使我们掌握构件承载力的计算。第三部分讨论杆件体系的组成规律及其内力和位移的问题。 四、《建筑力学》的学习方法 《建筑力学》是土建类专业的一门重要的专业基础课,学习时要注意理解它的基本原理,掌握它的分析问题的方法和解题思路,切忌死记硬背;还要多做练习,不做一定数量的习题是很难掌握《建筑力学》的概念、原理和分析方法的;另外对做题中出现的错误应认真分析,找出原因,及时纠正。 引 言 同时作用在物体上的一群力,称为力系。 对物体作用效果相同的力系称为等效力系。 物体在力系作用下,相对于地球静止或作匀速直线运动,称为平衡。它是物体运动的一种特殊形式。 建筑力学中把运动状态没有变化的特殊情况称为平衡状态。 满足平衡状态的力系称为平衡力系。 使物体在力系作用下处于平衡力系时应满足的条件,称为力系的平衡条件。 第一章 力的基本性质与物体的受力分析 第一节 基本概念 一、刚体的概念 在外力作用下,几何形状、尺寸的变化可忽略不计的物体,称为刚体。 二、力的概念 力是物体间相互的机械作用,这种相互作用会使物体的运动状态发生变化(外效应)或使物体发生变形(内效应)。 实践证明:力对物体的作用效果取决于力的三要素。 1. 力的大小 力的大小表明物体间相互作用的强弱程度。 2. 力的方向 力不但有大小,而且还有方向。 3. 力的作用点 当作用范围与物体相比很小时,可以近似地看作是一个点。 在描述一个力时,必须全面表明这个力的三要素。 力是矢量。

 用字母表示力矢量时,用黑体字F,普通体F只表示力矢量的大小。 用字母表示力矢量时,用黑体字F,普通体F只表示力矢量的大小。 第二节 静力学公理 一、力的平行四边形公理 作用于物体上同一点的两个力,可以合成为一个合力,合力的作用点也在该点,合力的大小和方向,由这两个力为边构成的平行四边形的对角线确定。 二、二力平衡公理 作用在同一刚体上的两个力,使刚体处于平衡的必要和充分条件是:这两个力大小相等,方向相反,且在同一直线上。 三、加减平衡力系公理 在已知力系上加上或减去任意的平衡力系,并不改变原力系对刚体的作用效果。也就是说,如果两个力系只相差一个或几个平衡力系,则它们对刚体的作用是相同的,可以等效代换。 推论1 力的可传性原理 作用在刚体上某点的力,可以沿着它的作用线移动到刚体内任意一点,而不改变该力对刚体的作用效果。 推论2 三力平衡汇交定理 作用于同一刚体上共面而不平行的三个力使刚体平衡时,则这 三个力的作用线必汇交于一点。 四、作用与反作用公理 两物体间的作用力与反作用力,总是大小相等、方向相反,沿同一直线并分别作用于两个物体上。 必须注意:不能把作用力与反作用力公理与二力平衡公理相混淆。 第三节 工程中常见的约束与约束反力 一、约束与约束反力的概念 对非自由体的某些位移起限制作用的周围物体称为约束体,简称约束。阻碍物体运动的力称为约束反力,简称反力。 所以,约束反力的方向必与该约束所能阻碍物体运动的方向相反。由此可以确定约束反力的方向或作用线的位置。 物体受到的力一般可以分为主动力、约束反力。 一般主动力是已知的,而约束反力是未知的。 二、几种常见的约束及其反力 1. 柔体约束 FT 2. 光滑接触面约束 FN 3. 圆柱铰链约束 4. 链杆约束 画出简图分别举例 三、支座及支座反力 工程中将结构或构件支承在基础或另一静止构件上的装置称为支座。建筑工程中常见的三种支座:固定铰支座(铰链支座)、可动铰支座和固定端支座。 1. 固定铰支座(铰链支座) 2. 可动铰支座 3. 固定端支座 画出简图分别举例 作 业:思考题5、6 复习 第四节物体的受力分析和受力图 物体的受力分析。 物体的受力图。受力图是进行力学计算的依据,也是解决力学问题的关键,必须认真对待,熟练掌握。 一、单个物体的受力图 例1 - 1、2、3 二、物体系统的受力图 物体系统的受力图与单个物体的受力图画法相同,只是研究对象可能是整个物体系统或系统的某一部分或某一物体。画物体系统整体的受力图时,只须把整体作为单个物体一样对待;画系统的某一部分或某一物体的受力图时,只须把研究对象从系统中分离出来,同时注意被拆开的联系处,有相应的约束反力,并应符合作用力与反作用力公理。 例1 - 4、5 受力图注意以下几点: 1. 必须明确研究对象。 2. 正确确定研究对象受力的数目。 3. 注意约束反力与约束类型相对应。 4. 注意作用力与反作用力之间的关系。 作 业:习题1、2、3 复习 【课程】2平面汇交力系 【教学要求】 掌握力在坐标轴上的投影及合力投影定理; 掌握平面汇交力系、平面一般力系的平衡条件; 【重 点】 掌握平面汇交力系、平面一般力系的平衡条件; 掌握物体系统的平衡条件。 【难 点】 平面汇交力系的解法 【授课方式】 课堂讲解加练习 【教学时数】 共计4学时 第二章 平面汇交力系 静力学是研究力系的合成和平衡问题。 平面汇交力系 平面力系 平面平行力系 力系 平面一般力系 空间力系 本章将用几何法、解析法来研究平面汇交力系的合成和平衡问题。 第一节平面汇交力系合成与平衡的几何法 一、平面汇交力系合成的几何法 1. 两个汇交力的合成。 平行四边形法则 三角形法则 2. 任意个汇交力的合成 结论:平面汇交力系合成的结果是一个合力,合力的大小和方向等于原力系中各力的矢量和,合力作用线通过原力系各力的汇交点。 例2 - 1 二、平面汇交力系平衡的几何条件 FR=ΣF=0 平面汇交力系平衡的几何条件为:力多边形自行闭合。 例2 - 2 例2 - 3 通过上述例题,可以总结出几何法求解平面汇交力系平衡问题的步骤如下: ⑴ 选取研究对象。根据题意选取与已知力和未知力有关的物体作为研究对象,并画出简图。 ⑵受力分析,画出受力图。在研究对象上画出全部已知力和未知力(包括约束反力)。注意运用二力杆的性质和三力平衡汇交定理来确定约束反力的作用线。当约束反力的指向未定时,可先假设。 ⑶ 作力多边形。选择适当的比例尺,作出封闭的力多边形。注意,作图时先画已知力,后画未知力,按力多边形法则和封闭特点,确定未知力的实际指向。 ⑷ 量出未知量。根据比例尺量出未知量。对于特殊角还可用三角公式计算得出。 作 业:题2----1、2、3 第二节平面汇交力系合成与平衡的解析法 几何法简捷、直观,但精确度有赖准确作图。 力学中常采用解析法。这种方法以力在坐标轴上投影的计算为基础。 一、平面汇交力系合成的解析法 1. 力在坐标轴上的投影 简图说明 投影符号正、负的规定:当从力始端投影到终端投影的方向与坐标轴的正向一致时,该投影取正值;反之,取负值。 两种特殊情形: ⑴当力与轴垂直时,投影为零。 ⑵当力与轴平行时,投影的绝对值等于力的大小。 投影与分力二者不可混淆。 例2 - 4 2. 合力投影定理 合力投影定理:合力在任一坐标轴上的投影等于各分力在同一坐标轴上投影的代数和。 3. 用解析法求平面汇交力系的合力
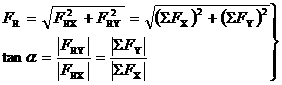 式中α为合力FR与x轴所夹的锐角。合力的作用线通过力系的汇交点O,合力FR的指向,由FRX和FRY(即ΣFX、ΣFY)的正负号来确定。 例2 - 5 二、平面汇交力系平衡的解析条件 由上节可知,平面汇交力系平衡的必要和充分条件是该力系的合力等于零。根据式(2-5)的第一式可知:
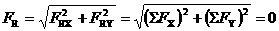 上式中(ΣFX)2与(ΣFY)2恒为正数。若使FR=0,必须同时满足 ΣFX=0 ΣFY=0 平面汇交力系平衡的必要和充分的解析条件是:力系中所有各力在两个坐标轴上投影的代数和分别等于零。 上式称为平面汇交力系的平衡方程。这是两个独立的方程,可以求解两个未知量。这一点与几何法相一致。 例2-6 例2-7 例2-8 通过以上各例的分析讨论,现将解析法求解平面汇交力系平衡问题时的步骤归纳如下: 1. 选取研究对象。 2. 画出研究对象的受力图。当约束反力的指向未定时,可先假设其指向。 3. 选取适当的坐标系。最好使坐标轴与某一个未知力垂直,以便简化计算。 4. 建立平衡方程求解未知力,尽量作到一个方程解一个未知量,避免解联立方程。列方程时注意各力的投影的正负号。求出的未知力带负号时,表示该力的实际指向与假设指向相反。 作 业:题2----4、5 【课程】3力矩和平面力偶系 【教学要求】 掌握力矩的概念及合力矩定理; 掌握力偶的性质;掌握物体系统的平衡条件。 【重 点】 掌握力偶系的平衡条件; 掌握物体系统的平衡条件。 【难 点】 力偶性质的利用,求物体系统的平衡时如何选取研究对象。 【授课方式】 课堂讲解加练习 【教学时数】 共计4学时 第三章 力对点的矩与平面力偶系 第一节 力对点的矩的概念及计算 一、力对点的矩 力F与距离d两者的乘积
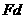 来量度力F对物体的转动效应。 来量度力F对物体的转动效应。 转动中心O称为力矩中心,简称矩心。 矩心到力作用线的垂直距离d,称为力臂。 改变力F绕O点转动的方向,作用效果也不同。 力F对物体绕O点转动的效应,由下列因素决定: (1)力的大小与力臂的乘积
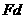 。 。 (2)力使物体绕O点的转动方向。 MO(F)=±
 通常规定:逆为正,反之为负。 在平面问题中,力矩为代数量。 力矩的单位:
 ( (
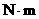 )或 )或
 ( (
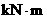 )。 )。 MO(F)=±2△AOB 力矩在下列两种情况下等于零: (1)力等于零; (2)力的作用线通过矩心,即力臂等于零。 二、合力矩定理 平面汇交力系的合力对平面内任一点的力矩,等于力系中各分力对同一点的力矩的代数和。这就是平面力系的合力矩定理。用公式表示为
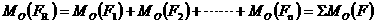 简单证明: 例3-1 例3-2 课堂练习(补充) 作 业:题3----1、2 【课程】4平面一般力系 【教学要求】 掌握平面一般力系的平衡条件; 掌握物体系统的平衡条件。 【重 点】 掌握平面一般力系的平衡条件; 掌握物体系统的平衡条件。 【难 点】 求物体系统的平衡时如何选取研究对象。 【授课方式】 课堂讲解加练习 【教学时数】 共计6学时 第四章 平面一般力系 平面一般力系是指各力的作用线在同一平面内但不全交于一点,也不全互相平行的力系。举例。 本章将讨论平面一般力系的简化与平衡问题,并以平衡问题为主。 第一节 平面一般力系向作用面内任一点简化 一、力的平移定理 由此可见,作用于物体上某点的力可以平移到此物体上的任一点,但必须附加一个力偶,其力偶矩等于原力对新作用点的矩,这就是力的平移定理。此定理只适用于刚体。 应用力的平移定理时,须注意下列两点: (一)平移力F'的大小与作用点位置无关。 (二)力的平移定理说明作用于物体上某点的一个力可以和作用于另外一点的一个力和一个力偶等效,反过来也可将同平面内的一个力和一个力偶化为一个合力 二、简化方法和结果 主矢
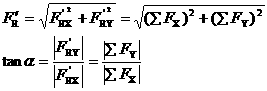 主矩 Mo′=M1+M2+…+Mn Mo′=Mo(F1)+Mo(F2)+…+Mo(Fn)=∑Mo(F) 综上所述可知:平面一般力系向作用面内任一点简化的结果,是一个力和一个力偶。这个力作用在简化中心,它的矢量称为原力系的主矢,并等于这个力系中各力的矢量和;这个力偶的力偶矩称为原力系对简化中心的主矩,并等于原力系中各力对简化中心的力矩的代数和。 主矢描述原力系对物体的平移作用; 主矩描述原力系对物体绕简化中心的转动作用,二者的作用总和才能代表原力系对物体的作用。 三、平面一般力系简化结果的讨论 1.若FR′=0,MO′≠0 一个力偶 2.若FR′≠0,Mo′=0 一个力 3.若FR′≠0,Mo′≠0 可继续简化:一个力 4.若FR′=0,Mo′=0 平衡(下节讨论) 四、平面力系的合力矩定理 Mo(FR)=∑Mo(F) 例4-1 例4-2 沿直线平行同向分布的线荷载,荷载合力的大小等于该荷载图的面积,方向与分布荷载同向,其作用线通过该荷载图的形心。 作 业:题4----1、2、3、4 第二节平面一般力系的平衡方程及其应用 一、平面一般力系的平衡条件与平衡方程 平面一般力系平衡方程的基本形式 ∑FX=0 ∑FY=0 ∑Mo(F)=0 二、平衡方程的其它形式 1.二力矩形式 ∑FX=0 ∑MA(F)=0 ∑MB(F)=0 式中x轴不可与A、B两点的连线垂直。 2.三力矩形式 ∑MA(F)= 0 ∑MB(F) = 0 ∑MC(F)= 0 式中A、B、C三点不共线。 三、平衡方程的应用 应用平面一般力系的平衡方程,主要是求解结构的约束反力,还可求解主动力之间的关系和物体的平衡位置等问题。其解题步骤如下: 1.确定研究对象。 2.分析受力并画出受力图。 3.列平衡方程求解未知量。 例4 -- 3 4 5 6 7 作 业:题4----5、6、8、10、12、 第三节 平面平行力系的平衡方程 平面力系中,各力的作用线互相平行时,称为平面平行力系。 平面平行力系的平衡方程为 ∑FY= 0 ∑MO(F)= 0 平面平行力系平衡方程的二力矩式 ∑MA(F)=0 ∑MB(F)=0 其中A、B两点的连线不与各力的作用线平行。 例4-8 例4-9 例4-10 作 业:题4----16、17 第四节 物体系统的平衡问题 在解决物体系统的平衡问题时,既可选整个系统为研究对象,也可选其中某个物体为研究对象,然后列出相应的平衡方程,以解出所需的未知量。 研究物体系统的平衡问题,不仅要求解支座反力,而且还需要计算系统内各物体之间的相互作用力。 应当注意:我们研究物体系统平衡问题时,要寻求解题的最佳方法。即以最少的计算过程,迅速而准确地求出未知力。其有效方法就是尽量避免解联立方程。一般情况下,通过合理地选取研究对象,以及恰当地列平衡方程及其形式,就能取得事半功倍的效果。而合理地选取研究对象,一般有两种方法: 1.。“先整体、后局部” 2.“先局部、后整体”或“先局部、后另一局部” 在整个计算过程中,当画整体、部分或单个物体的受力图时还应注意:①同一约束反力的方向和字母标记必须前后一致;②内部约束拆开后相互作用的力应符合作用与反作用规律;③不要把某物体上的力移到另一个物体上;④正确判断二力杆,以简化计算。 |